15. 표본분포
우선 표본 조사의 필요성과 표본 추출 방법에 대해서 배워보자
- 통계적 추론
- 표본조사를 통해 모집단에 대한 해석을 진행
- 전수조사는 실질적으로 불가능한 경우가 많음
- 표본조사는 반드시 오차가 발생
- 따라서 적절한 표본 추출 방법 필요
표본과 모집단의 관계를 이해해야 함
표본 추출 방법
- 단순랜덤추출법(Random sampling)
- 난수표 사용
- 랜덤 넘버 생성기 사용
표본분포
표본 평균의 분포
모수 (Parameter) : 표본조사를 통해 파악하고자 하는 정보
- 모수의 종류
- 모평균, 모분산, 모비율 등
- 모수를 추정하기 위해 표본을 선택하여 표본 평균이나 표본 분산 등을 계산
통계량 (statisic) : 표본 평균이나 표본 분산과 같은 표본의 특성값
Ex)
50만명의 전국 고등학교 1학년 학생의 키를 조사하기 위해 1000명을 표본 조사한다.
- 표본의 평균을 계산
- 표본의 평균은 표본의 선택에 따라 달라질 수 있음
따라서 표본평균은 확률변수이다.
(표본 평균이 가질 수 있는 값도 하나의 확률분포를 가지며, 이 분포가 무엇인지가 표본을 해석하는데 있어서 매우 중요)
표본분포 (sampling distribution) : 통계량의 확률분포
표본평균 : 모평균을 알아내는데 쓰이는 통계량

정리)
- 표본평균 \(\bar{X}\)는 정규분포를 따른다.
- 평균이 모집단에서의 평균(모평균)과 같다.
- \(n\)의 크기가 커질수록 분산이 작아진다. (\(\bar{X}\)가 평균에 가까워지는 값을 가지게 됨)
# 예시 1.


# 예시 2.



중심극한정리 (Central limit theorem)
모집단이 정규분포를 따르지 않는 경우가 있다. 그런 경우 중심극한정리 방법 사용해서 평균을 계산한다.

# 예시 1. 균일분포


\(n\) = 3 일 때,

\(n\) 값이 작기 때문에 아직 정규분포를 따르는 것이 아니다.
\(n\) = 10 일 때,

\(n\) = 30 일 때,
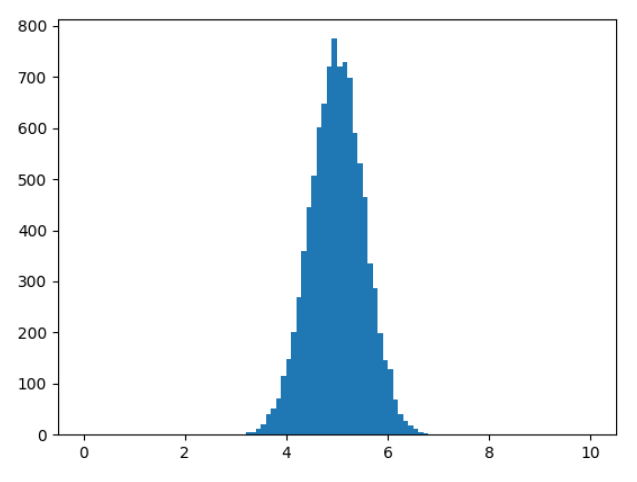
\(n\)이 커질수록 정규분포에 가까워짐
# 예시 2. 지수분포


\(n\) = 2 일 때,

\(n\) = 10 일 때,

\(n\) = 30 일 때,

\(n\)이 커질수록 정규분포에 가까워짐
정리)
- 여러가지 표본분포 중 표본평균의 분포만 살펴보았다.
- 표본평균에서 표본을 어떻게 추출하냐에 따라서 값이 달라진다. \(\rightarrow\) 확률변수
- 표본평균의 분포는 정규분포를 따른다.
- 모집단이 정규분포일 경우에는 \(n\) 의 크기에 상관없이 정규분포를 따른다.
- 모집단이 정규분포가 아닐 경우 \(n\)이 30 이상이면 중심극한정리에 따라서 정규분포를 따르게 된다.
16. 추정
- 모평균(모집단에서의 평균)의 추정
- 모비율(모집단에서의 비율)의 추정
모평균의 추정
표본평균의 특성

점추정

\(\Rightarrow\) 단순히 평균을 구하는 모평균을 추정함
(정확하게 모평균이 되는 것은 아니지만, 10개라는 제한적인 정보에서는 확률이 가장 높은 추정값이다.)
정리)
- 점추정만으로는 모평균이라고 추정하기에는 확실하지 않다.
- 따라서 구간추정을 이용
구간측정


- 표본평균을 이용하여 구간을 제시하고, 그 구간을 신뢰구간이라고 함.
(95%의 신뢰구간이라고 하면, 100번정도 실행했을 때 95번은 구간안에 들어갈 것이라고 보장함을 뜻함.)

\(\rightarrow\) 구간안에 모평균이 존재할 것이라고 추정함
But)
실용적이지 못함 \(\rightarrow\) 보통은 정규분포가 아니거나 표준편차가 알려져 있지 않음

# 예시 1.
어떤 학교의 고1 남학생의 평균키를 추정하기 위해 36명을 표본으로 추출하여 그 표본평균과
표본표준편차를 계산하여 그 결과가 다음과 같다.
$$ \bar{x} = 173.6, s = 3.6 $$
평균키에 대한 95% 신뢰구간 (confidence interval)을 구하시오

# 예시 2.
어떤 농장에서 생산된 계란 30개의 표본을 뽑았더니 그 무게가 다음과 같다.
\( w = [10,7, 11.7, 9.8, 11.4, 10.8, 9.9, 10.1, 8.8, 12.2, 11.0, 11.3, 11.1, 10.3, 10.0, 9.9, \)
\( 11.1, 11.7, 11.5, 9.1, 10.3, 8.6, 12.1, 10.0, 13.0, 9.2, 9.8, 9.3, 9.4, 9.6, 9.2 ] \)
계란의 평균 무게에 대한 95% 신뢰구간 (confidence interval)을 구하시오.


모비율의 추정
표본비율을 이용하여 모비율을 추정
점추정
- 확률변수 \(X\) : \(n\) 개의 표본에서 특정 속성을 갖는 표본의 개수
- 모비율 \(p\)의 점추정량
$$ \hat{p} = \frac{X}{n}$$
# 예시.
대학교 1학년생의 흡연율을 조사하기 위해 150명을 랜덤하게 선택하여 흡연여부를 조사하였다.
이 중 48명이 흡연을 하고 있었다. 이 대학교 1학년생의 흡연율의 평균을 점추정하시오.

구간추정

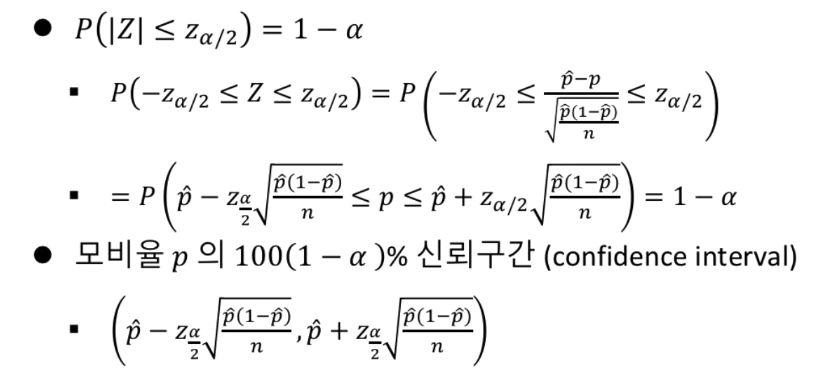
# 예시.
대학교 1학년생의 흡연율을 조사하기 위해 150명을 랜덤하게 선택하여 흡연여뷰를 조사하였다.
흡연율 \(p\)의 95% 신뢰구간 (Confidence interval)을 구하시오


17. 검정
- 통계적 가설검정
- 모평균의 검정
통계적 가설검정
가설검정이란?
어떤 고등학교의 1학년 학생들의 평균키가 170.5cm으로 알려져 있었다.
올해 새로 들어온 1학년 학생들 중 30명을 랜덤하게 선택하여 키를 잰 후
평균을 계산했더니 171.3cm이었다.
그렇다면, 올해 신입생은 평균키가 170.5cm보다 더 크다고 할 수 있는가?
\(\Rightarrow \) 이런 주장을 검증하는 것이 가설검정
- (표본평균 \(\bar{X}\) 가 \(\mu_{0}\) 보다 얼마나 커야 모평균 \(\mu\) 가 \(\mu_{0}\) 보다 크다고 할 수 있을까?)
표본평균은 표본의 선택에 의해 달라진다.
검정 원리
- 귀무가설
새로운 주장이 없었던 일이 됨- \(H_{0} \) : \(\mu = \mu_{0} \) (새로운 평균(표본평균)은 기존 평균과 같다.)
- 대립가설
새로운 주장이 맞음- \(H_{1} \) : \(\mu > \mu_{0}\) (\(or \mu < \mu_{0} \))
- 귀무가설을 기가하기 위해서는 \(\bar{X}\)가 조금 큰 값이 나와야 함( 그리고 그 확률이 낮아야 함)
- 귀무가설이 참이라는 가정하에, 랜덤하게 선택한 표본에서 지금의 \(\bar{X}\)가 나올 확률을 계산할 필요
- 이 확률이 낮다면 귀무가설이 참이 아니라고 판단
(위의 예시에서 171.3cm가 나올 확률이 낮다면 귀무가설은 기각)
\(\Rightarrow\) 귀무가설 기각 == 새로운 주장이 맞다.

검정 절차
- \(H_{0}, H_{1}\) 설정
- 유의수준 \(\alpha\) 설정
- 검정통계량 계산
- 기각역 또는 임계값 계산
- 주어진 데이터로부터 유의성 판정
모평균의 검정
모평균의 검정 방법
- 대립가설
- 검정통계량
- 기각역
대립가설
문제에서 검정하고자 하는 것이 무엇인지 파악 필요
- 대립가설 \(H_{1}\) 채택을 위한 통계적 증거 확보 필요
- 증거가 없으면 귀무가설 \(H_{0}\) 채택
- \(H_{1} : \mu > \mu_{0} \)
- \(H_{1} : \mu < \mu_{0} \)
- \(H_{1} : \mu \neq \mu_{0}\)
# 예시 1.
어떤 농장에서 생상되는 계란의 평균 무게는 10.5그램으로 알려져 있다.
i)
새로운 사료를 도입한 후에 생산된 계란 30개의 표본평균을 계산했더니 11.4그램이 나왔다.
새로운 사료가 평균적으로 더 무거운 계란을 생산한다고 할 수 있는가?
- \(H_{0} : \mu = 10.5 \)
- \(H_{1} : \mu > 10.5 \)
ii)
새로운 사료를 도입한 후에 생산된 계란 30개의 표본평균을 계산했더니 9.4그램이 나왔다.
새로운 사료가 평균적으로 더 가벼운 계란을 생산한다고 할 수 있는가?
- \(H_{0} : \mu = 10.5 \)
- \(H_{1} : \mu < 10.5 \)
# 예시 2.
어떤 농장에서 자신들이 생산하는 계란의 평균 무게가 10.5그램이라고 광고하고 있다.
이에 생산된 계란 30개의 표본 평균을 계산했더니 9.4그램이 나왔다.
이 농장의 광고가 맞다고 할 수 있나?
- \(H_{0} : \mu = 10.5 \)
- \(H_{1} : \mu \neq 10.5 \)
유의수준 \(\alpha\) 를 0.05로 설정하고 다음 절차 진행
검정통계량

기각역


# 예시.
어떤 농장에서 자신들이 생산하는 계란의 평균 무게가 10.5그램이라고 홍보하고 있다.
이에 생산된 계란 30개의 표본을 뽑았더니 그 무게가 다음과 같다.
\( w = [10,7, 11.7, 9.8, 11.4, 10.8, 9.9, 10.1, 8.8, 12.2, 11.0, 11.3, 11.1, 10.3, 10.0, 9.9, \)
\( 11.1, 11.7, 11.5, 9.1, 10.3, 8.6, 12.1, 10.0, 13.0, 9.2, 9.8, 9.3, 9.4, 9.6, 9.2 ] \)
이 농장의 홍보가 맞는지 유의 수준 5%로 검정하시오.



w의 모든 데이터에서 0.5 만큼 뺀다음 다시 진행해보기


18. 교차엔트로피
- 엔트로피
- 교차엔트로피
자기정보 (Self_information)
자기정보 : \(i(A)\)

확률이 낮은 사건이 정보가 많다.
두 사건 A, B가 동시에 일어났을 때의 자기정보 : \(i(AB)\)

\(\Rightarrow\) 각각의 자기정보를 합친 것과 같다.
# 예시.
동전을 던졌을 때 앞면이 나올 확률 H(head), 뒷면이 나올 확률 T(tail)

어떠한 사건에 대해서 그 사건이 발생할 확률을 가지고 정보의 량을 표현
엔트로피 (Entropy)
자기 정보의 평균 (Average of Self-Information)

- 엔트로피는 평균비트 수를 표현
- 데이터 압축에 사용 가능
# 예시.
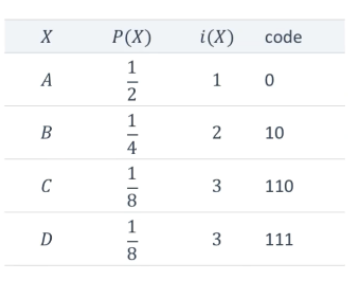
문자 A, B, C, D를 표현한다고 할 때, 4가지 정보를 표현하는데 필요한 비트 수 \(\rightarrow\) 2비트 필요
하지만 다음의 확률분포(밑의 표)에서 \(i(X)\)를 활용하는 경우
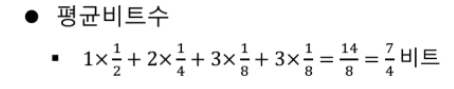
\(\Rightarrow\) 엔트로피는 데이터를 표현하는 데에 필요한 평균비트 수를 의미한다.
교차엔트로피
확률분포 P와 Q
- 사건의 집합 \(S = {A_{j}} \)
- \(P(A_{j}) \) : 확률분포 P에서 사건 A_{j}가 발생할 확률
- \(Q(A_{j}) \) : 확률분포 Q에서 사건 A_{j}가 발생할 확률
- \(i(A_{j}) \) : 확률분포 Q에서 사건 A_{j}의 자기정보
(여러 사건에 대한 확률분포 중에서, 일단 확률분포 Q에 따라서 정의)- \(i(A_{j}) = -\log_{2} Q(A_{j}) \)
- 자기정보는 \(A_{j}\)를 표현하는 비트 수
잘못된 확률분포 Q를 사용하게 되면, 실제 최적의 비트수를 사용하지 못하게 됨
교차엔트로피 H(P, Q)

# 예시.


교차엔트로피를 이용하면 두 확률분포 P와 Q가 얼마나 비슷한 지를 알 수 있다.
손실함수
- 분류 문제
- 주어진 대상이 A인지 아닌지를 판단
- 주어진 대상이 A, B, C, \(\dots\) 중 어느 것인지를 판단
- 기계학습에서는 주어진 대상이 각 그룹에 속할 확률을 제공
- 만약 [0.8, 0.2] (A일 확률이 0.8, 아닐 확률이 0.2) 라고 하면
이 값이 정답인 [1.0, 0.0] 과 얼마나 다른지 측정 필요
\(\rightarrow\) 이것을 측정하는 함수가 손실함수
- 만약 [0.8, 0.2] (A일 확률이 0.8, 아닐 확률이 0.2) 라고 하면
- 원하는 답 \(P = [p_1, p_2, \dots, p_n], p_1 + p_2 + \dots + p_n = 1 \)
- 제시된 답 \(Q = [q_1, q_2, \dots, q_n], q_1 + q_2 + \dots + q_n = 1 \)
P와 Q가 얼마나 다른지에 대한 척도 필요
손실함수 종류

분류 문제에서는 주로 교차 엔트로피 사용
분류문제에서의 원하는 답
- \(P = [p_1, p_2, \dots, p_n ])
- \(p_{i}\) 중 하나만 1이고, 나머지는 다 0임.
- \(p_{k} = 1.0\)이라고 하면, \(q_k\)의 값이 최대한 커지는 방향으로 학습 진행
# 예시.

\(\Rightarrow\) 원하는 답과 다른 수록 값이 커지게 됨


🔥 손실함수는 학습의 방향을 제공 (값이 0에 가까워지게끔)
'프로그래머스인공지능스쿨' 카테고리의 다른 글
| [3주차 - Day2] Python으로 데이터 다루기 I - numpy (0) | 2021.05.04 |
|---|---|
| [3주차 - Day2] 참고 : Git (0) | 2021.05.04 |
| [2주차 - Day4] 인공지능 수학 - 확률과 확률분포(2) (0) | 2021.04.29 |
| [2주차 - Day4] 인공지능 수학 - 확률과 확률분포(1) (0) | 2021.04.29 |
| [2주차 - Day3] 인공지능 수학 - 자료의 정리(2) (0) | 2021.04.29 |